SEGUNDO B: 2020

domingo, 14 de junio de 2020

ESTADISTICA

LINK PARA ENVIO DE PORTAFOLIO DIGITAL

SEGUNDO B

https://www.dropbox.com/request/aEVNtvZoBieI4eMBl2UK

TAREA N#14

Media (media aritmética)

La media es el valor que se obtiene al sumar todos los datos y dividir el resultado entre la cantidad de datos.

Su fórmula es la siguiente:

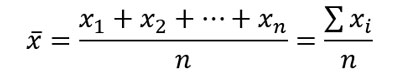media-mediana-y-moda-1 Aunque la fórmula parezca complicada, calcular el valor de la media es muy sencillo.

Ejemplo 1

Calcular la media de los siguientes datos: 11, 6, 7, 7, 4.

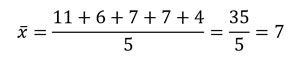
media-mediana-y-moda-2

Mediana

La mediana es el valor que ocupa la posición central cuando todos los datos están ordenados en orden creciente o decreciente.

La mediana se representa con las letras: Me.

Ejemplo 4

Calcular la mediana de los siguientes datos: 11, 6, 7, 7, 4.

Solución:

Ordenamos los datos de menor a mayor: 4, 6, 7, 7, 11.

Ahora tomamos el dato que se encuentra al centro: 4, 6, 7, 7, 11.

El valor de la mediana es: Me = 7.

¿Y si la cantidad de datos es un número par?

En ese caso, la mediana es la media entre los dos valores centrales.

Ejemplo 5

Calcular la mediana de los siguientes datos: 3, 6, 7, 9, 4, 4.

Solución:

Primero ordenamos los datos de menor a mayor: 3, 4, 4, 6, 7, 9.

La cantidad de datos es 6, es decir, un número par, así que vamos a ubicar los 2 valores centrales: 3, 4, 4, 6, 7, 9.

Entonces, la moda sería la media entre 4 y 6:

media-mediana-y-moda-5

Moda

La moda es el valor que más se repite. También podemos decir que la moda es el valor con mayor frecuencia absoluta o el valor que ocurre con más frecuencia.

La moda se representa con las letras: Mo.

Ejemplo 7

Calcular la moda de los siguientes datos: 11, 6, 7, 7, 4.

Podemos ver que el valor que más se repite es el 7, ya que tiene una frecuencia absoluta de 2, por lo tanto, Mo = 7.

DEBER

Encontrar la media, mediana y moda de los siguientes valores: 84; 91; 72; 68; 87; 78; 65; 87; 79.

domingo, 7 de junio de 2020

PARABOLA CON CENTRO (H,K)

TAREA N#13

Una parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco y de una recta fija del mismo plano llamada directriz.

La parábola es una sección cónica, resultado de la intersección de un cono recto con un plano que corta a la base del mismo, oblicuo a su eje y paralelo a una generatriz g de la superficie cónica.

El foco y la directriz determinan cómo va a ser la apariencia de la parábola (en el sentido de que “parecerá” más o menos abierta según sea la distancia entre F y la directriz). Todas las parábolas son semejantes. Su excentricidad es 1 en todos los casos. Solamente varía la escala.

Una de las aplicaciones físicas más importantes de la parábola es el movimiento parabólico. Este movimiento se caracteriza porque una partícula o cuerpo sólido lanzado en un campo gravitatorio recorre una trayectoria parabólica.

Una aplicación práctica de la parábola son las antenas parabólicas, en las que todas las rectas paralelas al eje de la parábola se reflejan en el foco de la misma. (Empleado en óptica, antenas de transmisión de radiofrecuencia, estufas domésticas parabólicas, captación de energía solar, etc.)

Elementos de una parábola

Los elementos de la parábola son:

Foco: el foco F es el punto fijo. Los puntos de la parábola equidistan del foco y la directriz.
Directriz: es la recta fija D. Los puntos de la parábola equidistan de la directriz y el foco.
Radio vector: es el segmento R que une el foco con cada uno de los puntos de la parábola. Es igual al segmento perpendicular a la directriz desde el punto correspondiente.
Eje: es la recta E perpendicular a la directriz que pasa por el foco y el vértice. Es el eje de simetría de la parábola.

Parámetro: es el vector p, que va desde el foco al punto más próximo de la directriz.
Es importante el signo del parámetro. En las parábolas verticales, cuando el parámetro es positivo la parábola se abre hacia arriba. Cuando p es negativo, la parábola se abre hacia abajo. Igualmente, en las parábolas horizontales, cuando p es positivo, se abre hacia la derecha y cuando p es negativo, la parábola se abre a la izquierda.
Vértice: es el punto V de la intersección del eje y la parábola.

Distancia focal: distancia entre el foco F y el vértice V. Es igual a p/2.

Puntos interiores y exteriores: la parábola divide el plano en dos regiones. Los puntos que están en la región del foco se llaman puntos interiores (I), mientras que los otros son los exteriores (J).

Cuerda: segmento que une dos puntos cualesquiera de la parábola.
Cuerda focal: una cuerda que pasa por el foco F.
Lado recto: Cuerda focal paralela a la directriz D y, por tanto, perpendicular al eje E. Su longitud es dos veces el parámetro (2p, pues se ven en la figura dos cuadrados unidos iguales de lado p).

Excentricidad de la parábola

La parábola es la única de las cónicas cuya excentricidad es siempre 1.

Veamos la figura.

Por la misma definición de parábola, su excentricidad siempre es la unidad. De esto deriva que todas las parábolas sean semejantes, variando su apariencia de cerradas o abiertas, según la escala.

Ecuación de la parábola

La ecuación de la parábola depende de si el eje es vertical u horizontal. Si el eje es vertical, la y será la variable dependiente. Si el eje es horizontal, será x la variable dependiente.

DEBER

1.-Determina los elementos de la parábola (vértice, foco, directriz, eje y lado recto) y

grafica

x² -2x -16y + 81 = 0

2.- Determina la ecuación general de la parábola cuyo vértice y foco son los puntos (-5, 2) y (-1, 2) respectivamente.

domingo, 31 de mayo de 2020

ECUACION DE LA PARABOLA REPASO

TAREA N#12

Una parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco y de una recta fija del mismo plano llamada directriz.

Elementos de una parábola

Los elementos de la parábola son:

Foco: el foco F es el punto fijo. Los puntos de la parábola equidistan del foco y la directriz.
Directriz: es la recta fija D. Los puntos de la parábola equidistan de la directriz y el foco.
Radio vector: es el segmento R que une el foco con cada uno de los puntos de la parábola. Es igual al segmento perpendicular a la directriz desde el punto correspondiente.
Eje: es la recta E perpendicular a la directriz que pasa por el foco y el vértice. Es el eje de simetría de la parábola.

Parámetro: es el vector p, que va desde el foco al punto más próximo de la directriz.
Es importante el signo del parámetro. En las parábolas verticales, cuando el parámetro es positivo la parábola se abre hacia arriba. Cuando p es negativo, la parábola se abre hacia abajo. Igualmente, en las parábolas horizontales, cuando p es positivo, se abre hacia la derecha y cuando p es negativo, la parábola se abre a la izquierda.
Vértice: es el punto V de la intersección del eje y la parábola.

Distancia focal: distancia entre el foco F y el vértice V. Es igual a p/2.

Cuerda: segmento que une dos puntos cualesquiera de la parábola.
Cuerda focal: una cuerda que pasa por el foco F.
Lado recto: Cuerda focal paralela a la directriz D y, por tanto, perpendicular al eje E. Su longitud es dos veces el parámetro (2p, pues se ven en la figura dos cuadrados unidos iguales de lado p).

Excentricidad de la parábola

La parábola es la única de las cónicas cuya excentricidad es siempre 1.

Veamos la figura.

Por la misma definición de parábola, su excentricidad siempre es la unidad. De esto deriva que todas las parábolas sean semejantes, variando su apariencia de cerradas o abiertas, según la escala.

Ecuación de la parábola

La ecuación de la parábola depende de si el eje es vertical u horizontal. Si el eje es vertical, la y será la variable dependiente. Si el eje es horizontal, será x la variable dependiente.

DEBER

1 En base a la ecuación de las siguientes parábolas determina las coordenadas de sus focos, ecuaciones de sus directrices, distancia de sus lados rectos y la gráfica.

$6y^2-12x=0$
$2y^2=-7x$
$15x^2=-42y$

lunes, 25 de mayo de 2020

Ecuacion de la Elipse con CENTRO (H, K)

TAREA #11

La ecuación de la elise con centro en el punto $C(h,k)$ es:

$\begin{equation*} \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1 \end{equation*}$

donde $a$ es la mitad de la longitud del eje mayor y $b$ es la mitad de la longitud del eje menor.

Geométricamente tenemos la siguiente situación:

Rendered by QuickLaTeX.com

Como era de esperarse, las fórmulas para el cálculo de los focos, sus vértices, etc. cambian. Por ejemplo, para calcular los vértices de la elipse horizontal, ahora utilizaremos las fórmulas:

La siguiente extensión al caso de la ecuación de la elipse en su primera forma ordinaria es considerar con centro fuera del origen, lo que nos lleva a la segunda forma ordinaria.

Contenido [Mostrar]

Ecuación de la elipse en su segunda forma ordinaria

La ecuación de la elise con centro en el punto $C(h,k)$ es:

$\begin{equation*} \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1 \end{equation*}$

donde $a$ es la mitad de la longitud del eje mayor y $b$ es la mitad de la longitud del eje menor.

Geométricamente tenemos la siguiente situación:

Rendered by QuickLaTeX.com

Como era de esperarse, las fórmulas para el cálculo de los focos, sus vértices, etc. cambian. Por ejemplo, para calcular los vértices de la elipse horizontal, ahora utilizaremos las fórmulas:

$\begin{eqnarray*} V(h + a, k) &\mbox{ y }& V'(h - a , k) \end{eqnarray*}$

Y para el caso de la elipse vertical tenemos:

$\begin{eqnarray*} V(h, k + a) &\mbox{ y }& V'(h , k - a) \end{eqnarray*}$

Por su parte los focos de la elipse horizontal se calculan con:

$\begin{eqnarray*} F(h + c,k) &\mbox{ y }& F'(h - c , k) \end{eqnarray*}$

Y para la elipse vertical:

$\begin{eqnarray*} F(h ,k + c) &\mbox{ y }& F'(h , k - c) \end{eqnarray*}$

Ejemplo 1

Calcula la ecuación de la elipse horizontal que tiene su centro en el punto $C(2,-1)$ y cuyo eje mayor mide 10 unidades y el eje menor mide 6 unidades.

Del texto del problema es facil ver que $h = 2$ y que $k = -1$ . También $a = 5$ y $b = 3$ . Luego, la ecuación de esta elipse es:

$\begin{equation*} \frac{(x - 2)^2}{25} + \frac{(y + 1)^2}{9} = 1 \end{equation*}$

A partir de los valores de $a$ y $b$ podemos calcular el valor de $c$ :

$\begin{equation*} c = \sqrt{a^2 - b^2} = \sqrt{25 - 16} = \sqrt{9} = 3 \end{equation*}$

Los focos de esta elipse están en los puntos:

$\begin{eqnarray*} F(h + c,k) = F(6,-1) &\mbox{ y }& F'(h - c , k) = F'(-2,-1) \end{eqnarray*}$

Los vértices están en:

$\begin{eqnarray*} V(h + a, k) = V(7,-1) &\mbox{ y }& V'(h - a, k) = V'(-3 , -1) \end{eqnarray*}$

La gráfica de esta elipse es la siguiente:

Rendered by QuickLaTeX.com

La excentricidad de esta elipse es:

$\begin{equation*} e = \frac{c}{a} = \frac{3}{5} = 0.6 \end{equation*}$

DEBER

. Hallar las coordenadas de los vértices, focos, LLR, excentricidad y la gráfica de la elipse cuya ecuación es

$\displaystyle \frac{{{\left( x-2 \right)}^{2}}}{9}+\frac{{{\left( y+1 \right)}^{2}}}{4}=1$