TAREA N#6
• Realizamos la siguiente actividad: en nuestro entorno, identificamos al menos 3 objetos que tengan la forma geométrica de una elipse. Leamos: • En las elipses con centro en el origen y eje de simetría x se cumple que:
Aplicamos el mismo procedimiento para obtener la ecuación de la elipse e identificamos que:
• Recordamos que a será el mayor valor en la ecuación de una elipse.
En este caso, como el valor mayor será el denominador de la fracción que tenga como numerador y^2, entonces se trata de una elipse con eje focal y.
• Realizamos un bosquejo de una elipse vertical y horizontal.
Podemos tomar como molde a los objetos que identificamos previamente.
Luego, en una hoja, graficamos dos planos cartesianos, y en cada uno graficamos la elipse vertical y horizontal, respectivamente, centradas en el origen.
Finalmente, escribamos el nombre que corresponda a cada elipse, es decir, “elipse con eje focal y” o “elipse con eje focal x”.
• Aplicamos las fórmulas revisadas en el ejemplo 11 y en el ejemplo 12 de la página 176.
EjemploHallar los elementos característicos y la ecuación reducida de la elipse de focos: F'(-3,0) y F(3, 0), y su eje mayor mide 10.

Semieje mayor
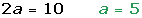
Semidistancia focal
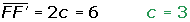
Semieje menor
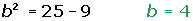
Ecuación reducida
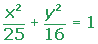
DEBER
Realizamos el ejercicio 12 y 13 de la página 176 del texto.
No hay comentarios.:
Publicar un comentario