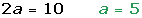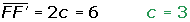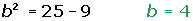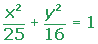La Parábola

TAREA 7

 Ecuaciones de la parábola. Reconocer analítica y gráficamente una parábola y sus elementos
● Contestamos(CUADERNO), en familia, las siguientes preguntas:
 o ¿Han visto alguna antena? o ¿Cuántas y en qué lugar las vieron? o ¿Qué forma geométrica tienen las antenas? Específicamente, de acuerdo con la lectura sobre Antenas Parabólicas en la página 196 del texto, ¿tú conocías la figura geométrica que mejor representa a este tipo de antenas.
Ecuación canónica de la parábola Una parábola es el lugar geométrico de todos los puntos de un plano que tienen una distancia igual a una recta fija, denominada directriz, y a un punto fijo, llamado foco.
 A continuación se resume los elementos que podemos apreciar en la parábola de acuerdo con el elemento del Eje de Simetría o Eje Focal, junto con sus respectivas características.
Aplicamos las fórmulas revisadas en el ejemplo 18 de la página 183 y en el ejemplo 20 de la página 184 del texto.



DEBER

• Realizamos un bosquejo, en tu cuaderno, de elementos del entorno con una configuración geométrica de una parábola en el plano cartesiano, identificando si son del tipo con eje de simetría al eje x o con eje de simetría al eje y.
 • Realizamos, en tu cuaderno, un resumen sobre este tema detallando sus elementos, y las gráficas correspondientes. Para esto, puedes usar la tabla presentada. •
Revisamos, si es posible, el contenido de los siguientes enlaces:

https://es.khanacademy.org/math/algebra/x2f8bb115 95b61c86:quadratic-functionsequations/x2f8bb11595b61c86:quadratic-formsfeatures/v/quadratic-functions-2

Ecuación canónica de la elipse con centro(0,0) y ejefocal

TAREA N#6

• Realizamos la siguiente actividad: en nuestro entorno, identificamos al menos 3 objetos que tengan la forma geométrica de una elipse. Leamos: • En las elipses con centro en el origen y eje de simetría x se cumple que:

Aplicamos el mismo procedimiento para obtener la ecuación de la elipse e identificamos que:
 • Recordamos que a será el mayor valor en la ecuación de una elipse.
En este caso, como el valor mayor será el denominador de la fracción que tenga como numerador y^2, entonces se trata de una elipse con eje focal y.
 • Realizamos un bosquejo de una elipse vertical y horizontal.
 Podemos tomar como molde a los objetos que identificamos previamente.
Luego, en una hoja, graficamos dos planos cartesianos, y en cada uno graficamos la elipse vertical y horizontal, respectivamente, centradas en el origen.
Finalmente, escribamos el nombre que corresponda a cada elipse, es decir, “elipse con eje focal y” o “elipse con eje focal x”.
• Aplicamos las fórmulas revisadas en el ejemplo 11 y en el ejemplo 12 de la página 176.

EjemploHallar los elementos característicos y la ecuación reducida de la elipse de focos: F'(-3,0) y F(3, 0), y su eje mayor mide 10.

Semieje mayor

Semidistancia focal

Semieje menor

Ecuación reducida

DEBER
Realizamos el ejercicio 12 y 13 de la página 176 del texto.

Verificación de la ecuación general de la circunferencia

DEBER N 5

1Contestamos las siguientes preguntas(CUADERNO DE MATEMÁTICA):
 ¿Qué característica tiene la ecuación canónica de una circunferencia?
 ¿Qué característica tiene la ecuación general de una circunferencia?
2 Analizamos la siguiente información, a partir de la ecuación general de una circunferencia:
 ¿cómo determinaríamos las coordenadas de su centro y el valor del radio?

● Recordamos que, si una ecuación general representa una circunferencia, entonces, podemos hallar las coordenadas de su centro y el valor de su radio.

 También podemos hallarlo transformando esta ecuación en la ecuación canónica de la circunferencia.

DEBER

 ● Aplicamos las fórmulas revisadas en esta clase y en la anterior al ejemplo 8 de la página 171. ● 

Resolvamos en el cuaderno el ejercicio 8 y el ejercicio 9 de la sección Ejercicios y problemas de la página 192 del texto.

Ecuación general de la circunferencia

TAREA #4 

Tema: Ecuación general de la circunferencia 

1 Contestamos la siguiente pregunta:(CUADERNO)
 ¿podríamos graficar una circunferencia sólo conociendo su radio? Justificamos la respuesta.
 2 Analizamos la siguiente información:
si desarrollamos la ecuación canónica de la recta, destruyendo los paréntesis, obtenemos la ecuación general de la recta así:
Ejemplos:

Analizamos el ejemplo 6 de la página 166 del texto para comprender la aplicación de la fórmula cuadrática.
DEBER(CUADERNO)
 • Resolvamos en el cuaderno los ejercicios 5 y 6 de la página 166 del texto.